Los problemas conocidos como problemas del camino mínimo o camino más corto, tratan como su nombre indica de hallar la ruta mínima o más corta entre dos puntos. Este mínimo puede ser la distancia entre los puntos origen y destino o bien el tiempo transcurrido para trasladarse desde un punto a otro. Se aplica mucho para problemas de redes de comunicaciones.
Este tipo de problemas pueden ser resueltos por el método del Simplex, sin embargo existen otros métodos más eficientes como por ejemplo el algoritmo de Dijkstra o el de Bellman-Ford.
Aquí les muestro un ejemplo en el siguiente video:
EL ALGORITMO DE DIJKSTRA
Descripción:
El algoritmo de dijkstra determina la ruta más corta desde un nodo origen hacia los demás nodos para ello es requerido como entrada un grafo cuyas aristas posean pesos. Algunas consideraciones:
Si los pesos de mis aristas son de valor 1, entonces bastará con usar el algoritmo de BFS.
Si los pesos de mis aristas son negativos no puedo usar el algoritmo de dijsktra, para pesos negativos tenemos otro algoritmo llamado Algoritmo de Bellmand-Ford.
Como trabaja:
Primero marcamos todos los vértices como no utilizados. El algoritmo parte de un vértice origen que será ingresado, a partir de ese vértices evaluaremos sus adyacentes, como dijkstra usa una técnica greedy - La técnica greedy utiliza el principio de que para que un camino sea óptimo, todos los caminos que contiene también deben ser óptimos- entre todos los vértices adyacentes, buscamos el que esté más cerca de nuestro punto origen, lo tomamos como punto intermedio y vemos si podemos llegar más rápido a través de este vértice a los demás. Después escogemos al siguiente más cercano (con las distancias ya actualizadas) y repetimos el proceso. Esto lo hacemos hasta que el vértice no utilizado más cercano sea nuestro destino. Al proceso de actualizar las distancias tomando como punto intermedio al nuevo vértice se le conoce como relajación.
En múltiples aplicaciones donde se aplican los grafos, es necesario conocer el camino de menor costo entre dos vértices dados:
Distribución de productos a una red de establecimientos comerciales.
Distribución de correos postales.
Sea G = (V, A) un grafo dirigido ponderado.
El problema del camino más corto de un vértice a otro consiste en determinar el camino de menor costo, desde un vértice u a otro vértice v. El costo de un camino es la suma de los costos (pesos) de los arcos que lo conforman.
Características del algoritmo
Es un algoritmo greddy.
Trabaja por etapas, y toma en cada etapa la mejor solución sin considerar consecuencias futuras.
El óptimo encontrado en una etapa puede modificarse posteriormente si surge una solución mejor.
Pasos del algoritmo
Algoritmo de Dijkstra. Inicialización.
Sea V un conjunto de vértices de un grafo.
Sea C una matriz de costos de las aristas del grafo, donde en C[u,v] se almacena el costo de la arista entre u y v.
Sea S un conjunto que contendrá los vértices para los cuales ya se tiene determinado el camino mínimo.
Sea D un arreglo unidimensional tal que D[v] es el costo del camino mínimo del vértice origen al vértice v.
Sea P un arreglo unidimensional tal que P[v] es el vértice predecesor de v en el camino mínimo que se tiene construido.
Sea vinicial el vértice origen. Recordar que el Algoritmo Dijkstra determina los caminos mínimos que existen partiendo de un vértice origen al resto de los vértices.
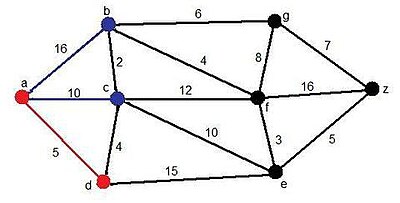
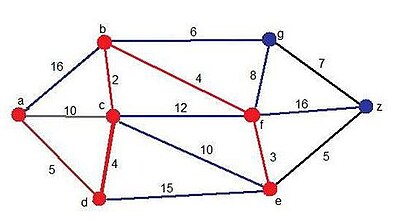
El siguiente ejemplo se desarrollará con el fin de encontrar el camino más corto desde a hasta z:
Leyenda:
Rojo: Aristas y vértices pertenecientes a la solución momentánea.
Azul: Aristas y vértices candidatos.
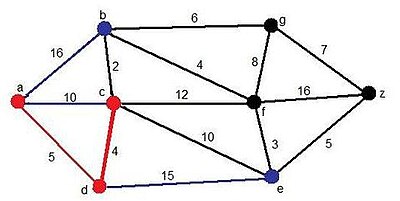
Paso 2
Ahora, vemos que se añade un nuevo candidato, el vértice e, y el vértice c, pero esta vez a través del d. Pero el camino mínimo surge al añadir el vértice c.
Solución momentánea:
Camino: ADC
Distancia:9
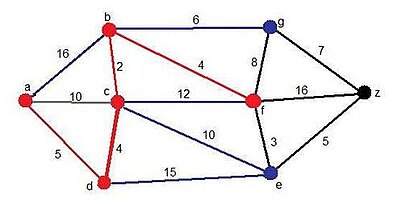
Paso 3
En este paso se añade como candidato el vértice f. En este caso el camino mínimo hallado es el siguiente:
Solución momentánea:
Camino: ADCB
Distancia:11
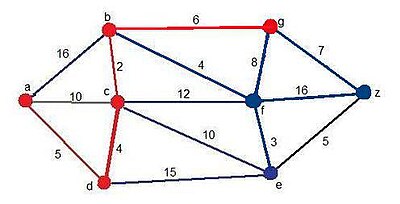
Paso 4
Como podemos comprobar, se han añadido un candidato nuevo, el vértice g, a través del vértice b. El mínimo camino hallado en todo el grafo hasta ahora es el siguiente:
Solución momentánea:
Camino: ADCBF
Distancia:15
Paso 5
En este antepenúltimo paso, se añaden tres vértices candidatos, los vértices g, z y e. Este último ya estaba pero en esta ocasión aparece a través del vértice f. En este caso el camino mínimo, que cambia un poco con respecto al enterior, es:
Solución momentánea:
Camino: ADCBG
Distancia:17
Paso 6
En el penúltimo paso, vuelve a aparecer otro candidato: el vértice e, pero esta vez a través del vértice f. De todas formas, el camino mínimo vuelve a cambiar para retomar el camino que venía siguiendo en los pasos anteriores:
Solución momentánea:
Camino: ADCBFE
Distancia:18
Paso 7
Por fin, llegamos al último paso, en el que sólo se añade un candidato, el vértice z a través del e. El camino mínimo y final obtenido es nada mas y nada menos k:
Solución Final:
Camino: ADCBFEZ
Distancia:23
Aquí les dejo otro Ejemplo en video:



No hay comentarios:
Publicar un comentario